티스토리 뷰
//재귀를 이용한 완전탐색.
function solve(pos, visited) {
if (visited == (1 << N )- 1) return 0;
let ret = min;
for (let next = 0; next < N; next++) {
if (!(visited & (1 << next)) && Graph[pos][next] != 0) {
let temp = Graph[pos][next] + solve(next, visited|(1 << next));
if (temp < ret) ret = temp;
}
}
return ret;
}
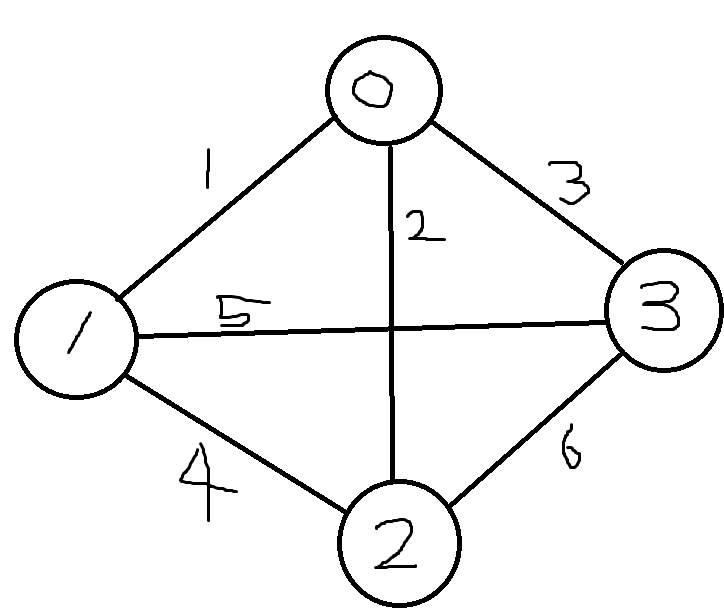
let Graph = [
[0, 1, 2, 3],
[1, 0, 4, 5],
[2, 4, 0, 6],
[3, 5, 6, 0]];
let N = Graph.length;
let min = 99999999;
for (let i = 0; i < N;i++) {
let temp = solve(i, 1 << i);
if (min > temp) min = temp;
}
console.log(min);- 그래프는 인접행렬로 표현
- N은 노드 개수
- min은 모든 간선의 비용을 모두 더한 값보다 큰 값. 엄청 큰 값을 주면된다.
- for문에서 solve(0, 0000) solve(1, 0010). solve(2, 0100), solve(3,1000); 이해를 돕기위해 visited는 2진수로 나타냈다.
- solve(0,0)부터 시작하여 재귀방식으로 수행.
- if (visited == (1 << N )- 1) return 0; 모든 노드를 방문했다면 종료.
- if (!(visited & (1 << next)) && Graph[pos][next] != 0) 방문하지 않는 노드일 경우 && 방문가능한 노드일 경우 수행한다. 위 예제는 완전그래프라서 방문가능한 노드인지 굳이 확인할 필요는 없다.
- 현재 노드에서 방문한 노드까지의 간선의 비용을 더하고 solve() 재귀.
728x90
공지사항
최근에 올라온 글
최근에 달린 댓글
- Total
- Today
- Yesterday
링크
TAG
- 로드나인
- 그래프
- create databases;
- 롱베케이션
- 면접질문
- 서버개발
- node.js
- 서버점검
- 다이나믹프로그래밍
- 동적프로그래밍
- 개발자면접
- MOD
- MySQL
- 투포인터 연습
- 최소공통조상
- DB 생성
- create db
- 은둔청년체험
- 다이나밍프로그래밍
- KMP
- 투포인터
- BFS
- 면접비
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
글 보관함
